# LeetCode

# 二分查找

# 基础题目

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

编号 704.

解析来自:

https://www.programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#_704-%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE

思路:

定义一个left索引和right索引来记录整个数组的查找区间,循环查找区间

在循环中,首先比较left与right的值,判断区间是否存在,如果right小于left,返回-1;若区间存在通过left和right计算middle索引,并通过middle获取值value,与target比较;

若value等于target,直接返回值
若value大于target,则代表target在left与middle范围中,不包含middle
若value小于target,则代表target在middle与right范围中,同样不包含middle

查找区间可分两种: 左闭右闭 [left,right] 左闭右开[left,right)

左闭右闭

// 左闭右闭
public static int search(int[] nums, int target) {
    int left = 0, right = nums.length -1;
    // [left,right]
    while (left <= right){
        int middle = (right + left) / 2;
        int value = nums [middle];
        if (target > value) {
            left = middle + 1;
        } else if (target < value) {
            right = middle - 1;
        } else {
            return middle;
        }
    }
    return -1;
}

左闭右开

// 左闭右开
public static int search(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // [left,right)
    while (left < right) {
        int middle = (right + left) / 2;
        int value = nums[middle];
        if (target > value) {
            left = middle + 1;
        } else if (target < value) {
            right = middle;
        } else {
            return middle;
        }
    }
    return -1;
}

总结:

二分法最重要的就是区间的判断左闭右闭还是左闭右开

while循环条件以及right边界值的修改,都是根据区间来判断的

# 第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

编号 278.

思路:

可以将版本看成一个数组,这个数组同样满足二分查找的条件

定义查找区间:第一个和最后一个都有可能是第一个出bug的版本,因此两个版本都要包含

调用api 查看middle是否有bug

有bug 代表middle之后都有bug, middle还是在查找区间中, right 等于 middle
无bug 代表middle之前都无bug, middle就不在查找区间中,left 等于 middle+1

left 之前都无bug,left之后都有bug

当left与right相等时,那个值就是第一个出现bug的版本

public static int firstBadVersion(int n) {
    
    int left = 1, right = n;
    while (left < right) {
        int middle = left + (right - left) / 2;
        boolean result1 = isBadVersion(middle);
        if (result1) {
            right = middle + 1;
        } else {
            left = middle;
        }
    }
    return left;
}

# 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

编号 35.

思路:

这道题与普通的二分查找,区别在于目标值不存在于数组的情况下的处理

普通的二分查找只要返回-1

这道题要返回按顺序插入的位置,也就是当区间不成立时,返回边界的值

例如

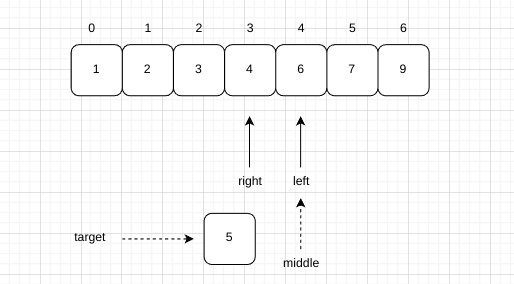
此时区间不成立,循环结束,返回left 或者 right+1

public static int searchInsert(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // []
    while (left <= right) {
        int middle = left + (right - left) / 2;
        int num = nums[middle];
        if (target > num) {
            left = middle + 1;
        } else if (target < num) {
            right = middle - 1;
        } else {
            return middle;
        }
    }
    return right + 1;
}

# 双指针

# 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100] 排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

思路:

原数组带有负数,并已按照递增排序,因此每个数平方后的新数组,是先递增再递减的顺序

此时可以使用双指针,分别遍历数组

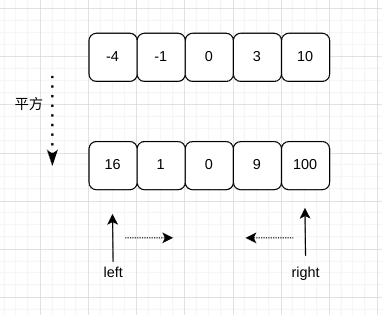
left与right遍历时,得到的皆为递增数组,在双指针遍历时,对两个指针获取到的值进行比较,大的值存入新数组最后一位,并移动指针,另一方不能移动

public static int[] sorted(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        nums[i] = nums[i] * nums[i];
    }
    // 新数组
    int[] newList = new int[nums.length];
    // 新数组插入元素的索引
    int k = newList.length - 1;
    
    // 双指针
    for (int i = 0, j = nums.length - 1; i <= j; ) {
        if (nums[i] > nums[j]){
            newList[k] = nums[i];
            i++;
        }else {
            newList[k] = nums[j];
            j--;
        }
        k--;
    }
    return newList;
}

← 基础篇数据结构 →